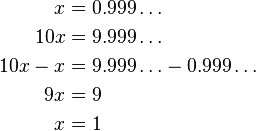در اینجا من به شما ۳ رقم و یک نتیجه خواهم داد، شما باید با قرار دادن علامت های صحیح معادله را کامل کنید.

برای درک بهتر ابتدا یک مثال را با هم حل میکنیم، باقی معادله ها به عهده ی شماست:

۲ + ۲ + ۲ = ۶

ساده بود نه؟ حالا بقیه ی معادله ها را حل کنید.

۱ ۱ ۱ = ۶

۲ ۲ ۲ = ۶

۳ ۳ ۳ = ۶

۴ ۴ ۴ = ۶

۵ ۵ ۵ = ۶

۶ ۶ ۶ = ۶

۷ ۷ ۷ = ۶

۸ ۸ ۸ = ۶

۹ ۹ ۹ = ۶

.

.

.

خب؟ تونستید حل کنید؟

چی؟ فقط دومی رو؟! اون که مثال خودم بود…

و ششمی رو؟ وای خدای من! خیلی سخت بود نه؟!

۶ + ۶ – ۶ = ۶

نابغه!!!

بقیه چه طور؟

کمک می خوای؟

اوه! معلومه که نه! پاک فراموش کرده بودم شما یک نابغه هستی…

حدس می زنم که از عهده ی سومی هم بر اومدی

۳ × ۳ – ۳ = ۶

شاید از عهده ی پنجمی

۵ / ۵ + ۵ = ۶

و با یه کم شانس هفتمی…

-۷ / ۷ + ۷ = ۶

هنوز به نظرت غلطه؟ ببین:

– (۷/۷) = -۱

و در نتیجه

۷ – ۱ = ۶

حالا میریم سراغ اونها که یه کم مشکل تر به نظر میان…

ریاضیات به عنوان یک درس اصلی است که داشتن درک درست از آن در آینده ی تحصیلی دانش آموزان و طبعاً پیشرفت علمی کشور نقش مهمی دارد . همچنین شامل کلیه ارتباطات ریاضی با زندگی روزمرّه ، سایر علوم و کاربردهایی در زندگی علمی آینده ی دانش آموزاست .به این ترتیب دربرنامه درسی و آموزشی ، برقرار کردن پیوند ریاضیات با کاربردهایش در زندگی و سایر علوم از قبیل :هنر،علوم طبیعی ،علوم اجتماعی و . . . . باید مدّ نظر قرار گیرد . در صورتی که این موارد در آموزش دیده نشود ، این سؤ ال همیشه در ذهن دانش آموز باقی می ماند که:

« به چه دلیل باید ریاضی خواند ؟ » و« ریاضی به چه درد می خورد ؟ »

دراین مقاله سعی شده است که ارتباط دروس کتب ریاضی راهنمایی با سایر علوم و همچنین کاربرد آنها در دنیای امروز ی تا حدودی بررسی شود و ارائه گردد .

بین رشته های علمی ، که بشر در طول هزاران سال به وجود آورده ، ریاضیّات جای مخصوص و ضمناٌ مهمّی را اشغال کرده است . ریاضیّات با علوم فیزیک ، زیست شناسی ، اقتصاد و فنون مختلف فرق دارد . با وجود این به عنوان یکی از روشهای اصلی در بررسیهای مربوط به کامپیوتر ، فیزیک ، زیست شناسی ، صنعت واقتصاد بکار می رود ودرآینده بازهم نقش ریاضّیات گسترش بیشتری می یابد.

با وجود این مطلب ، برای آموزش جوانان هنوز از همان روشی استفاده می شود که سقراط و افلاطون ، حقایق عالی اخلاقی را برای شیفتگان منطق و فلسفه و برای علاقمندان سخنوری و علم کلام بیان می کردند . در حقیقت در درسهای حساب ، هندسه و جبر ،هرگز لزوم یادگیری آنها برای زندگی عملی خاطر نشان نمی شود. هرگز از تاریخ علم صحبتی به میان نمی آید. نظریه های سنگین علمی ، ولی هیچ نتیجه ای جز این ندارد که دانش آموزان را از علم بری کند و عدّه ی آنها را تقلیل دهد .

یکی ازراههای جدی برای حلّ مسئله توجه به تاریخ علم، گفتگو در باره ی مردان علم و ارتباط ریاضی با عمل است ، ارتباطی که در تمام دوران زندگی بشر هرگز قطع نشده است .

● کاربرد ارقام

در زمانهای قدیم هر قدمی که در راه پیشرفت تمدّن برداشته می-شد، بر لزوم استفاده از اعداد می افزود . اگر شخصی گله ای از گوسفندان داشت ، می خواست آن را بشمرد ،یا اگر می خواست معبد یا هرمی بسازد ، باید می دانست که چقدر سنگ برای آن لازم دارد . اگر دارای زمین بود ، می خواست آن رااندازه گیری کند . اگر قایقش را به دریا می راند ، می خواست فاصله ی خود را از ساحل بداند . و بالاخره در تجارت و مبادله ی اجناس در بازارها ، باید ارزش اجناس حساب می شد.هنگامی که آدمی محاسبه با ارقام را آموخت ، توانست زمان ، فاصله مساحت ، حجم را اندازه گیری کند . با بکار بردن ارقام ، انسان بردانش و تسلّط خود بر دنیای پیرامونش افزود .

● کاربرد توابع و روابط بین اعداد

کاربرد روابط بین اعداد و توابع و نتیجه گیریهای منطقی در نوشتن الگوریتمها و برنامه نویسی کامپیوتری است .

مفهوم تابع یکی از مهمترین مفاهیم ریاضی است و در اصل تابع نوعی خاص از رابطه های بین دو مجموعه است . و با توجه به این که دنباله ها هم حالت خاصی از تابع است - تابعی که دامنه آن مجموعه ی اعداد { . . . و ۲ و ۱ و ۰ } است - دنباله های عددی در ریاضی و کامپیوتر کاربرد فراوان دارند . برای ساخت یک برنامه اساساٌ چهار مرحله را طی می کنیم :

۱) تعریف مسئله

۲) طراحی حل

۳) نوشتن برنامه

۴) اجرای برنامه

لازم به ذکر است که گردآیه هایی که در مرحله دوم حاصل می شود را اصطلاحاٌ الگوریتم می نامیم .که این الگوریتمهابه زبان شبه کد نوشته می شود ،که شبیه زبان برنامه نویسی است وتبدیل آنها به زبان برنامه نویسی را برای ما بسیار ساده می کند .

 « هیچ دانسته ی بشر را نمی توان علم نامید، مگر اینکه از طریق ریاضیّات توضیح داده شده و ثابت شود . » ( لئو ناردو داوینچی )

● کاربرد معادله و دستگاه معادلات خطی

دستگاه های معادلات خطی اغلب برای حساب کردن بهره ی ساده ،پیشگویی ، اقتصاد و پیدا کردن نقطه ی سر به سر به کارمیرود.

معمولاً هدف از حل کردن یک دستگاه معادلات خطی ، پیدا کردن محل تقاطع دو خط می باشد.در مسائل دخل و خرج که درمشاغل مختلف وجود دارد ، پیداکردن نقطه تقاطع معادلات خط یعنی همان پیدا کردن نقطه ی سر به سر.* در اقتصاد هم نقطه تقاطع معادلات خطی ، عبارتست از : قیمت بازار یا نقطه ای که در آن عرضه و تقاضا با هم برابر باشند.

● کاربرد تقارنها (محوری و مرکزی ) و دورانها

مباحث تقارنها ودورانها که به تبدیلات هندسی معروف هستند،درصنعت و ساختن وسائل و لوازم زندگی استفاده می شوند . مثلاً در بافتن قالی و برای دادن نقش و نگار به آن از تقارن استفاده می شود . در کوزه گری و سفالگری از دوران محوری استفاده می - شود . همچنین در معماریهای اسلامی اغلب از تقارنها کمک گرفته می شود . چرخ گوشت ، آب میوه گیری ، پنکه ، ماشین تراش ُ بادورانی که انجام می دهند ، تبدیل انرژی می کنند . علاوه بر آن تبدیلات هندسی برای آموزش مطالبی از ریاضی استفاده می شوند ،مانند : مفهوم جمع و تفریق اعداد صحیح با استفاده از بردار انتقال موازی محور.

▪ نقطه ی سر به سر : در بسیاری از مشاغل ، هزینه ی تولید Cو تعداد X کالای تولید شده را می توان به صورت خطی بیان کرد.به همین ترتیب ، در آمد R حاصل از فروش X قلم کالای تولیدشده را نیز می توان با یک معادله ی خطی نشان داد . وقتی هزینه ی C از در آمد R حاصل از فروش بیشتر باشد،این تولیدضررمی دهد. و وقتی در آمد R از هزینه ی C بیشتر باشد ،تولید سودمیدهد . و هر گاه در آمد R و هزینه ی C مساوی باشند ،سود و زیانی در بین نیست و نقطه ای که در آن R=C باشد، نقطه ی سربه سر نامیده می شود .

● کاربرد مساحت

مفهوم مساحت و تکنیک محاسبه مساحت اشکال مختلف ، از اهمّ مطالب هندسه است .به سبب کاربرد فراوانی که در زندگی روزمرّه مثلاً برای محاسبه ی مساحت زمینها با اَشکال مختلف . و همچنین درفیزیک و جغرافیاوسایر دروس دانستن مساحتهالازم به نظرمی رسد .

● کاربرد چهار ضلعیها

شناخت چهارضلعیها و و دانستن خواص آنها ، برای یادگیری مفاهیم دیگر هندسه لازم است و ضمناً در صنعت و ساخت ابزار و وسائل زندگی و همچنین برای ادامه تحصیل وهمینطور در بازار کار نیاز به دانستن خواص چهارضلعیها احساس می شود .

● کاربرد خطوط موازی و تشابهات

از خطوط موازی و مخصوصاً متساوی الفاصله ، در نقشه کشی و ترسیمات استفاده می شود .و در اثبات احکامی نظیر قضیه تالس۱ و عکس آن ، همچنین تقسیم پاره خط به قطعات متساوی یامتناسب .

تشابهات نیز از مفاهیم مهم هندسه و اساس نقشه برداری ،کوچک و بزرگ کردن نقشه ها و تصاویر و عکسها می باشد .

مبحث تشابهات درهندسه دریچه ای است به توانائیهای جدیدبرای درک و فهم و کشف مطالب تازه ی هندسه ،به همین سبب آموزش خطوطمتوازی و متساوی الفاصله و مثلثهای متشابه به حد نیاز دانش-

آموز مقطع راهنمایی لازم است .

۱) تالس دانشمند یونانی نشان داد که به وسیله ی سایه ی یک شیء و مقایسه ی آن با سایه ی یک خط کش می توان ارتفاع آن  شیء را اندازه گرفت . با استفاده از اصولی که تالس ثابت کرد ،می توان بلندی هر چیزی را حساب کرد . تنها چیزی که نیاز دارید ، یک وسیله ی ساده اندازه گیری است که می توانید[آن را ] از یک قطعه مقواو تکه ای چوب درست کنید.( مراجعه شودبه کتاب درجهان ریاضیات نوشته ی اریک او بلاکر - صفحه ی ۳۰ )

تالس در زمان خود به کمک قضیه ی خودارتفاع اهرام مصررامحاسبه کرد همچنین وقتی از مصر به یونان بازگشت ، فاصله ی یک کشتی را از ساحل به کمک قضیه خود اندازه گرفت .روش دیگری هم برای

محاسبه بلندی وجود دارد وآن استفاده از نسبتهای مثلثاتی است.

 ● کاربرد آمار و میانگین

وقتی کسی از مقادیر عددی کمک می گیرد ، تا یک موقعیّت را توضیح دهد ، او وارد قلمرو آمار شده است . آمار معمولاً اثر تعیین کننده ای دارد . اگر چه ممکن است مفید یا گمراه کننده باشد . ما عادت کرده ایم، که پدیده های زیادی نظیرموارد زیر را با توجه به آمار ، پیش بینی کنیم :

احتمال پیروزی یک کاندیدای ریاست جمهوری،وضعیت اقتصادی(تورم،در آمد ناخالص ملی ، تعداد بیکاران ،کم وزیادشدن نرخ بهره هاونرخ سهام ، بازار بورس ، میزان بیمه ، آمار طوفان،جذر و مد) و غیره .

قلمرو آمار به طور مرتب درحال بزرگ شدن است.آمار می توانددر موارد زیادی ، برای قانع کردن مردم و یا انصراف آنهااز یک تصمیم موءثّر باشد . به عنوان مثال : اگر افراداحساس کنند که رأی آنها نتیجه ی انتخابات را تغییر نخواهد داد ، ممکن است ازشرکت در انتخابات صرفنظر کنند .

در عصر ما آمار ابزار قوی و قانع کننده است،مردم به اعدادمنتشر شده ی حاصل از آمار گیری ،اعتماد زیادی نشان می دهند.

به نظر می رسد وقتی یک وضعیت وموقعیت باتوسل به مقادیر عددی توصیف می شود ، اعتبار گزارش در نظر مستمعین بالا می رود .

● مقاطع مخروطی

در هوای گرم بستنی بسیار خوشمزه ودلچسب است .بخصوص اگر بستنی قیفی داشته باشید ودر حالی که روی یک صندلی و در سایه درختی نشسته باشید و فارغ از جار و جنجال روزگار ، به خوردن بستنی  مشغول باشید. شاید همه چیز از ذهن شما بگذردمگرهمان بستنی قیفی که مشغول خوردن آن هستید .

این مطلب توجه یک ریاضیدان بلژیکی خوش ذوق رابه خودجلب کرد و آن رابرای توضیح یکی ازمطالب مهم ریاضی[یعنی مقاطع مخروطی]بکار برد . واقعاً جالب است مگه نه ؟

مقاطع مخروطی یکی از مباحث مهم و کاربردی در ریاضیات بوده وهست .

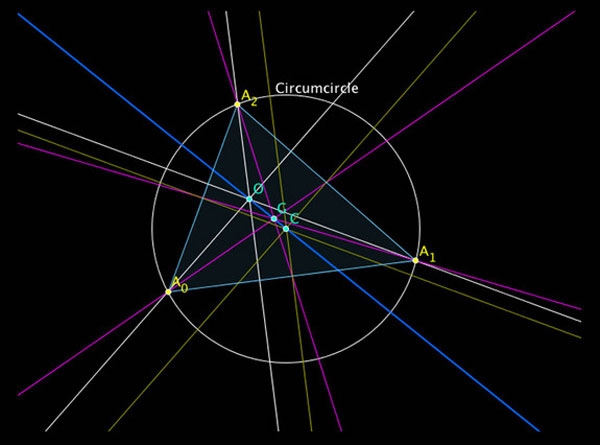
● ترسیمات هندسی

در ترسیمات و آموزش قسمتهای دیگر هندسه، نیاز فراوان به شناخت دایره و اجزاو خواص آن پیدا می شود ، لذا در دوره ی راهنمایی ، مفهوم دایره ،وضع نقطه و خط نسبت به دایره،زاویه مرکزی ، زاویه محاطی و تقسیم دایره به کمانهای متساوی آموزش داده می شود و به این ترتیب دانش آموز برای یادگیری مطالب بعدی و استفاده ی عملی از آنها آماده می شود . (همچنین من فکرمیکنم از زاویه ی محاطی و اندازه ی آن برای نورپردازی در سالنهااستفاده می شود . )

● کاربرد ریاضیات در هنر و کامپیوتر

تاریخ نشان می دهد که در طی قرون ، هنرمندان وآثارشان تحت تأثیرریاضیات قرار گرفته اند ،و زیبائی اثرشان به آگاهی آنها از این دانش بستگی داشته است .ماهم اکنون استفاده ی آگاهانه از مستطیل طلایی ، و نسبت طلایی را در هنر یونان باستان ، به ویژه درآثارپیکرتراش یونانی« فیدیاس »دقیقآ مشاهده می کنیم.

مفاهیم ریاضی از قبیل نسبتها ، تشابه، پرسپکتیو، خطای باصره تقارن ، اشکال هندسی ، حدود و بینهایت در آثار هنری موجوداز قدیم تا به امروز مکمل زیبایی آنها بوده است . و اکنون نیز « کامپیوتر » به کمک ریاضیات هنر را ازابتدایی تامدرن توسعه می دهد.

اگر آگاهی هنرمندان باریاضیات واستفاده ی عملی از ان نبود،برخی از آثار هنری خلق نمی شدند . بهترین نمونه ی آن تصاویر موزائیکی هنرمندن مسلمان وگسترش این شکلهای هندسی به وسیله ی

« M.S.Esher » جهت نشان دادن اجسام متحرک است .اگر هنرمندان به مطالعات توجهی نداشتندوخصوصیات اشکال را از نظر تطابق،تقارن انعکاس ،دوران ، انتقال و . . . کشف نکرده بودند ، خلق این همه آثار هنری امکان پذیر نبود .

« هنر ریاضیات ،هنرپرسیدنِِِ پرسشهای درست است وقطعه ی اصلی کار در ریاضیات تخیل است و آن چه که این قطعه ی اصلی رابه حرکت درمی آوردمنطق می باشدوامکان استدلال

منطقی آن زمان پدید می آیدکه ما پرسشهای خود رادرست مطرح کرده باشیم.» (نوربرت ونیز )

● کاربرد حجم

به سبب نیازی که دانش آموز در زندگی روز مرّه و همین طور در بکار گیری آن در سایر علوم نظیر ، شیمی ، فیزیک ،زیست شناسی و مخصوصاً هنر برایش پیش می آید،همچنین در شغلهایی که در جامعه وجود دارد و یا در ادامه تحصیل دانستن دستورهای محاسبه ی حجماجسام ، یادگیری مبحث حجم ضروری به نظر می رسد .

● کاربرد رابطه ی فیثاغورس

فیثاغورث در باره ی رابطه های عددی که درساختمانهای هندسی وجود دارد تحقیق می کرد . او مثلث معروف به مثلث مصری را ، که ضلعهای آن با عددهای ۳و۴و ۵ بیان می شود ، را می شناخت .

مصریها می دانستند که چنین مثلثی قائم الزاویه است .و ازآن برای تعیین زاویه های قائمه در تجدید تقسیم بندی زمینهای اطراف نیل ،که هر سال بر اثر طغیان آب شسته می شد ، استفاده می کردند.

یکی از مشکلترین مسائل در ساختن اهرام و معبدها ،طرح شالوده بنا به شکل مربع کامل بود که هم تراز باسطح افق باشد . جزئی اشتباه به قیمت از شکل افتادن همه ی بنا تمام می شد .

مصریان این مشکل رابا ساختن شاقول از میان برداشتند. نخستین شاقول احتمالاً تکه ریسمان یا نخی بود که وزنه ای به آن آویخته بودند و ان را در برابر بنا می گرفتند تا وزنه ی آن به زمین صاف برسد . در این حالت نخ می بایست کاملاً عمودیا شاقول باشد و زاویه ی بین آن و زمین صاف یک زاویه ی قائمه بسازد.

همچنین معماران کشف کردندکه چگونه می توان با ریسمان های اندازه گیری که درفاصله های مساوی گره خورده بودند، مثلثهای قائم الزاویه ای بسازند و این مثلثها را راهنمای خویش در ساختن گوشه ها ( نبش ها )ی بنا قرار دهند .

● جمع بندی و نتیجه گیری

بدون شک مهمترین هدف ما از بیان مطالب بالا این است که بتوانیم دانش آموزان را با اهداف کتب ریاضی آشنا کنیم و آنها را نسبت به ریاضیات علاقمند کنیم . تجربه نشان داده است که حتی در رشته های فنی ، مانند خیاطی هم اهداف پرورشی ریاضی اهمیت دارند به همین خاطر دربرنامه ی درسی تمام رشته های تحصیلی درس ریاضی گنجانده شده است .

در کتب جدید ریاضی سعی شده است که مطالب طوری بیان شوند که دانش آموز نفهمیده مطلبی را نپذیرد.هر چند بعضی مطالب شهودی است.ولی دانش آموز از طریق درک مفاهیم درس یاد می گیرد و به

تدریج با فرایندتفکر ریاضی آشنا می شود .معلمین هم باید به این نکته توجه داشته باشند و تصور نکنند که هدف آموزش ریاضی فقط در یاد دادن چند قاعده و حل ماشینی مسائل خلاصه می شود 

 

منبع : www.aftab.ir - آفتاب

تجسم یک شعر

تا حالا شعر کانکریت خوانده اید ؟ نه ؟ البته نیازی به ناراحتی نیست چون شعری که در بالا خواندید یک شعر کانکریت یا تجسمی است ! پیشنهاد می کنم شعر را دوباره بخوانید و دوباره ببینید ! چون هر باری که بخوانید زیباییش بیشتر دیده میشه !

منبع : وبلاگ سبوی تشنه

راه هایی برای آموزش بهتر ریاضی به دختران

برگزیده شدن مریم میرزاخانی، دانشمند ایرانی به عنوان برنده جایزه انجمن ریاضیات امریکا، تنها یکی از خبرهایی است که این روزها از موفقیت دانشمندان زن ایرانی می شنویم. این در حالی است که هنوز در قرن 21، این باور عمومی وجود دارد که پسران بهتر از دختران ریاضیات را می فهمند.

تحقیقات نشان داده است، عقب تر بودن دختران در درک مفاهیم ریاضی، علی رغم تصور عمومی، مربوط به ژنتیک نیست بلکه موضوعی کاملا فرهنگی است. در این گزارش راهکارهایی برای آموزش این دانش به دختران پیشنهاد شده است.

نتایج تحقیقاتی اخیرا گاردین منتشر کرده است، نشان می دهد که دختران اگر در محیط مناسبی رشد کنند از توانایی برابر و حتی بالاتری نسبت به پسران در ریاضیات برخوردارند. چگونه می توان شرایط را برای شکوفایی استعداد های دختران در این زمینه ها فراهم کرد؟

دختران بهتر از پسران

مطالعات نشان می دهد که عملکرد دختران 15 ساله نسبت به پسران هم سن و سال خود در بسیاری از کشور ها کیفیت بالاتری دارد. محققان در یافته اند که اگر دختران در مناطقی عملکرد ضعیف تری در ریاضیات و علم از خود نشان می دهند دلیل آن محیط اجتماعی است.

تاکید بر عوامل اجتماعی در مورد ضعف ریاضیات در دختران امر جدیدی نیست. آخرین ازمون ریاضی که از برنامه ارزیابی بین المللی دانش آموزان، نتایج مشابهی در بر دارد. در برخی از کشور ها دختران پانزده ساله از پسران همسن و سال خود نمره برابر یا بالاتری گرفته اند. به لحاظ ژنتیکی آزمون ها نشان می دهند دختران تا حد زیادی قابلیت ریاضی دان شدن دارند. محققین سپس یافتند "در کشور هایی که پایین ترین مرتبه را از حیث برابری جنسیتی دارد بیشترین شکاف در عملکرد ریاضی دختران و پسران وجود دارد".

طبق نتایج دپارتمان آموزش امریکا، دخترانی که اعتماد بیشتری نسبت به توانایی های خود در ریاضیات و علم دارند بیشتر متمایل اند تا ریاضیات و علوم را انتخاب کنند و عملکرد بهتری خواهند داشت و مشاغل و رشته های ریاضی و علم محور را انتخاب خواهند کرد.

دپارتمان تاکید کرده است که ارتقای باورهای دختران درباره توانایی هایشان می تواند انتخاب ها و عملکرد های آنها را تغییر دهد. علی الخصوص زمانی که آنها از مدرسه ابتدایی وارد راهنمایی و دبیرستان می شوند.

اگر طبیعت بر توانایی دختران تاثیری نمی گذارد، چه عاملی موجب این تغییرات می شود؟ در اینجا چندین نکته از نظر متخصصین وجود دارد:

به دختر بچه ها تاکید کنیم که در جهانی علمی زندگی می کنیم
محققین در یک کنفرانس در باب علم در نیویورک چندین سال قبل بیان کردند که دختران به طور فزاینده ای درمقابل ایده "علم" موضع می گیرند و آن را همچون یک موضوع سخت و صلب رد می کرنند، در حالیکه آنها زمانی که تحت عنوان "علوم اجتماعی" به آنها آموزانده می شود بطور عجیبی مفتون همان اصول می شوند.

پیش بینی هوا، تغییرات جوی، آنچه می خوریم مریضی ها و حساسیت ها روش های نقل مکان برقی که تمام خانه ما را پر کرده، تمام حوزه های علم است که دنیای دختر ها را نیز محاصره کرده است. باید برای دختر بچه ها در این باره توضیح داد و اینگونه او را با علم و ریاضیات آشنا ساخت. نظریه علمی تخیل او را تحریک می کند زمانیکه به فعالیت های کنونی و خانگی مربوط می شوند.

دختران و نیمکره چپ مغز
دختران عموما پردازش اطلاعات را در قسمت چپ مغز که قسمت زبانیِ مغز انجام می دهند. با این حال دختران مفاهیم ریاضی را به طور زبانی ساختارکاوی می کنند. نگاه به چیزی روی سطح یا صفحه برای آنها کافی نیست. آنها باید درباره مسئله صحبت کنند. آنها باید درباره آن حرف بزنند.

دختران درباره رنگ نسبت به پسران حساسیت بیشتری دارند
استفاده از اسباب بازی های رنگ بندی شده و بلوک رنگی برای دسته بندی الگوها باید از سنین ابتدایی شروع شود. بلوک رنگی بخرید و با کودکانتان با آنها الگو بسازید.

از کد های رنگی بیشتر استفاده کنید
این بازی را با این ایده ترکیب کنید که چطور در خانه اشیا را می توان بر اساس رنگ سامان داد. درباره اینکه چگونه عمل دسته بندی را انجام می دهید، برای دخترتان صحبت کنید . تا برای کارهایی که برای اشیای رنگی انجام می دهید روایتی ساخته باشید . تقویم خانه خود را رنگی کنید و بر اساس رنگ ها از او تاریخ ها را بخواهید.

بلند خواندن دستورالعمل ها
آیا دخترتان دستورالعمل ها و نسخه های بازی ها، دستگاه ها، و دستور پخت غذا را بلند می خواند؟ وقتی کودک نهایتا این تجارب خانگی را انجام دهد، قادر خواهد بود تا مسیر های پیموده شده را در این میان دریابد. این تجربیات همچنین وی را قادر می سازد تا مسائل پیچیده تر را با شکستن به مسائل کوچکتر بررسی و نتیجه گیری نماید.

کیت های آموزشی
زمانی که دختربچه شما در ساختن بلوک های رنگی و الگو سازی تبحر یافت، برای او کیت بخرید. چرا که در کیت ها ساختن بر مبنای اجرای از روی دستور العمل رخ می دهد. حتی زمانیکه برنامه تا حد زیادی ساده است او را مجبور کنید تا سیر انجام کار را بلند توضیح دهد. توجه کردن به اینکه در این روایت کلامی دختر بچه ها چه مراحلی را از قلم می اندازند جالب است.

او را تشویق کنید که با قلب خود بیاموزد
گاهی دخترها زمانی که چیزی را متوجه نمی شوند آن را حفظ می کنند. اگر چه ممکن است شما ترجیح دهید که او آن را دریابد و بفهمد ولی گاهی همین به حافظه سپردن ( مانند جدول ضرب) قدم مهمی در کشف الگو ها محسوب می شود.

از دخترتان بخواهید که شکلی را از روی یک طرح بکشد و یا برای وی چیزی را تعریف کنید تا طرح آن را ترسیم کند

از وی بخواهید تصویری را ببیند و که شما نمی توانید ببینید و برای شما تعریف کند تا بتوانید آن را ترسیم کنید. از این طریق شما می توانید پیوند بین تصویر و کلمه را در ذهن وی قوت ببخشید؛ یا در واقع رابطه بین زبان و تصویر سازی را.

استفاده از پازل
پازل ها از رده فعالیت های بسیار مهم و مفید برای تقویت ذهن هستند. آنها الزایمر را به تاخیر می اندازند. جدول کلمات متقاطع نیز از این قسم اند.

هر گز پاسخ را به کودک خود نگویید
نکته مهمی که در حل مسئله ریاضی وجود دارد آن است که نیازی نیست که تمرین ریاضی دخترها، حتما منجر به حل جواب شود بلکه همین که کودک بتواند مسیر حل مسئله را تشخیص دهد قدم بزرگی محسوب می شود. اگر دخترتان بر روی مسئله ای اصطلاحا گیر کرده است نه وی را رها کنید و نه به او پاسخ را بگویید. بلکه وی را با سوالات متعدد به پرسش بکشید." چه کار باید کرد؟"، " چطور می توان را ساده تر کرد؟" و از این قبیل .

آشپزی، دنبال کردن دستورالعمل، استفاده توامان از علم و ریاضیات
وزن کردن، اندازه گیری و زمان سنجی همگی تمرین های ریاضیاتی هستند. پخت و پز بخصوص زمانی که می توان دید عمل الف روی ماده ب منجر به چیزی به نام ج می شود یک مقوله علمی محسوب می شود. اگر دخترها را تشویق کنید تا در اشپزخانه به تجربه کردن بپردازند، آزمایشات بیشتری در مدرسه انجام خواهد داد.

البته نکات دیگری نیز وجود دارد که می توان برای توسعه توانایی هایی دختر بچه ها به کار گرفت:

عباراتی نظیر اینکه "من در این کار خوب نیستم" یا "ریاضی من خوب نیست " را از آنها نپذیرید.

- کودک باید از خانه به مدرسه توانایی های خود را گسترش دهد. در واقع خانه باید اولین جا برای برخورد با مسائل ریاضیاتی علمی کتاب و ادوات الکترونیکی باشد.

- آنها را تشویق کنید کمتر تلویزیون ببینند و بیشتر کتاب بخوانند.

- به آنها الگوهای مناسبی از زنان ریاضیدان و دانشمند معرفی کنید.

منبع : عصر ایران

محبوب ترین معادلات ریاضی برای دانشمندان

 معادلات ریاضی نه تنها کاربردی، بلکه بسیار زیبا هستند و دانشمندان زیادی اذعان کرده‌اند که اغلب آنها شیفته فرمولهای خاص نه به دلیل کاربرد بلکه به دلیل فرم و حقایق ساده و شاعرانه درونشان می‌شوند.
  در حالیکه برخی معادلات مشهور مانند معادل‌بودن جرم با انرژی، یا E = mc^2 اینشتین بیشتر افتخار بشری را به خود اختصاص داده‌اند، بسیاری از فرمولهای کمتر شناخته شده از اهمیت خاص خود در میان دانشمندان برخوردارند.
در این پست از فیزیکدانان، ستاره‌شناسان و ریاضیدانان در مورد معادلات مورد علاقه آنها سوال شده و برترین‌ها به نمایش درآمده است.

- نسبیت عام
این معادله توسط اینشتین به عنوان بخشی از نظریه چشمگیر نسبیت عام در سال 1915 طراحی شد. این نظریه درک دانشمندان را از گرانش با توصیف نیرو به عنوان یک خمیدگی تار و پود فضا و زمان متحول کرد.
ماریو لیویو، فیزیک‌اخترشناس موسسه علمی تلسکوپ فضایی که این معادله را عنوان معادله محبوب خود معرفی کرده، اظهار کرد. بخش راست این معادله به توصیف محتویات انرژی جهان مانند ماده تاریک و بخش چپ آن به هندسه فضا-زمان پرداخته است. این معادله این حقیقت را منعکس می‌کند که در نسبیت عام اینشتین، جرم و انرژی به تعیین هندسه و بطور همزمان انحنا پرداخته که یکی از مظاهر آنچه گرانش می‌خوانیم، است.

- مدل استاندارد
مدل استاندارد یکی دیگر از نظریات حاکم بر فیزیک است که مجموعه ذرات بنیادی سازنده جهان را توصیف می‌کند. این نظریه را می‌توان در مدل استاندارد لاگرانژی قرار داد.
این در حالیست که مدل استاندارد هنوز با نظریه نسبیت متحد نشده و از آن جهت نمی‌تواند گرانش را توصیف کند.

- حسابان
در حالیکه دو معادله اول جنبه‌های خاص جهان را توصیف می‌کنند، معادله دیگر مورد علاقه دانشمندان می‌تواند بر تمامی شکلهای شرایط اعمال شود. قضیه بنیادی حسابان، ستون اصلی شیوه ریاضیاتی حساب و دیفرانسیل را تشکیل داده و دو ایده اصلی آن یعنی مفهوم انتگرال و مشتق را مرتبط می‌کند.
پایه‌های حسابان در روزگاران قدیم چیده شده اما بسیاری از آن در قرن 17 میلادی توسط نیوتون در کنار هم قرار گرفت که از حسابان برای توصیف حرکات سیارات در اطراف خورشید استفاده کرده است.

- قضیه فیثاغورث
یکی از معادلات قدیمی اما خوب، قضیه معروف فیثاغورث است که تمام دانش‌آموزان با آن یادگیری هندسه را آغاز می‌کنند.
این فرمول به توضیح این مطلب می‌پردازد که در هر مثلث قائم‌الزاویه، توان دوم طول وتر(بلندترین ضلع مثلث) با جمع توان دوم طول دو ضلع دیگر برابر است.

- 1=0.9999999
این معادله ساده که مقدار 0.9999 را که با تعداد بی‌نهایت از 9 دنبال شده، مساوی با یک می‌داند، یکی دیگر از معادلات محبوب دانشمندان بوده است.

- نسبیت خاص
اینشتین یکبار دیگر نام خود را در لیست مورد علاقه‌ها با فرمول نسبیت خاص تکرار کرده که بر اساس آن مفاهیم فضا و زمان مطلق نبوده بلکه بر اساس سرعت مشاهده‌گر تا حدی مرتبط هستند. این معادله نشان می‌دهد که هرچه سرعت فرد در هر جهت بیشتر باشد، زمان آهسته‌تر می‌شود.

- معادله اویلر-لاگرانژ یا معادله اویلر
این فرمول ساده در نوع خود، موردی ناب درباره ذات کره است. اگر سطح یک کره را به وجوه، لبه‌ها و رئوس تقسیم کرده و F را بعنوان عدد وجوه، E را برای لبه‌ها و V را برای عدد رئوس انتخاب کنیم، همیشه این معادله را خواهیم داشت:

V – E + F = 2

- قضیه ی نوتر
قضیه نوتر بر این اساس است که برای هر تقارن پیوسته ای، کمیت پایسته ای در سیستم وجود دارد. این فرمول که شکل جدیدت معادله لاگرانژی است، پس از قرن 20 میلادی توسط امی نوتر، ریاضیدان آلمانی طراحی شده است. این فرمول برای فیزیک و نقش تقارن بسیار اهمیت دارد.

- معادله کالان - سیمانزیک
مت استراسلر، فیزیکدان نظری دانشگاه راتگرز اظهار کرد: معادله کالان-سیمانزیک یکی از معادلات اساسی اصول اول از سال 1970 بوده که برای توصیف چگونگی شکست انتظارات ساده در یک جهان کوانتومی نقش مهمی داشت.
این معادله از کاربردهای زیادی مانند ارزیابی اندازه و جرم پروتون و نوترون توسط فیزیکدانان برخوردار است.
فیزیک پایه بر این اساس است که نیروی گرانشی و نیروی الکتریکی بین دو جسم با معکوس مجذور فاصله بین آنها متناسب است. در یک سطح ساده، این امر برای نیروی اتمی نیرومندی که پروتونها و نوترونها را برای شکل‌دادن به هسته اتمها پیوند داده، نیز مشابه است. با این حال، نوسانات ریز کوانتومی می‌تواند وابستگی یک نیرو به مسافت را تغییر داده که عواقب چشمگیری بر نیروی قدرتمند اتمی دارد.
آنچه معادله کالان-سیمانزیک انجام می‌دهد، ارتباط دادن این تاثیر چشمگیر و غیرقابل محاسبه به تاثیرات کوچکتر و قابل محاسبه‌تر با قابلیت سنجش در مقیاسهای کوچکتر از پروتون است.

- معادله سطح حداقل
در ریاضیات، سطح حداقل به سطحی گفته می‌شود که بصورت محلی خود را کوچک می‌کند. این امر برابر با داشتن یک میانگین انحنای صفر است.

- خط اویلر
خط اویلر نشان می دهد در هر مثلث مرکز ارتفاعی، مرکز دایره محیطی و مرکز ثقل بر یک خط واقع هستند و این پاره خط توسط مرکز ثقل به نسبت 2 بر 1 تقسیم می شود.
گلن ویتنی، موسس موزه ریاضی در نیویورک این معادله را به عنوان فرمول محبوب خود انتخاب کرده که نام خود را از لئونارد ایولر، ریاضیدان و فیزیکدان سوئیسی در قرن 18 گرفته است.
به گفته ویتنی این نظریه دربرگیرنده زیبایی و قدرت ریاضی بوده که اغلب الگوهای شگفت‌انگیز را در شکلهای ساده و آشنا به نمایش می‌گذارد.

گروه سه نفر رياضي دانان هندي براي غلبه بر مشكل به هر دري زدند و با بررسي مقالات مختلف بالاخره دريافتند كه در سال ‪ ۱۹۸۵‬يك رياضي‌دان فرانسوي به نام اتن فووري از دانشگاه پاريس ‪ ۱۱‬اين نكته را به صورت رياضي اثبات كرده است. به اين ترتيب آخرين بخش معما حل شد و آلگوريتم پيشنهادي اين سه نفر با موفقيت پا به عرصه گذارد.

اما اين موفقيت "مشروط" بود. به اين معني كه اين روش براي اعداد اولي كه انسان در حال حاضر مي‌توان به سراغ آنها برود از كارآيي چنداني برخوردار نيست. در روايت اوليه روش پيشنهادي، زمان لازم براي محاسبات كه متناسب با ارقام عدد اول مورد نظر بود، با آهنگ ‪ ۱۰۱۲‬ازدياد پيدا مي كرد.

در روايتهاي بهبود يافته اخير اين روش، سرعت ازدياد زمان لازم براي محاسبات به ‪ ۱۰۷.۵‬كاهش يافته اما حتي در اين حالت نيز اين روش در مقايسه با روش آ پي آر تنها در هنگامي موثر تر خواهد بود كه تعداد ارقام عدد اولي كه قصد شكار و يافتن آن را داريم در حدود ‪ ۱۰۱۰۰۰‬باشد.

اعدادي تا اين اندازه بزرگ در حافظه هيچ كامپيوتر جاي نمي‌گيرند و حتي آن را نمي‌توان در كل كيهان جاي داد.

اما حال كه رياضي دانان توانسته‌اند يك طبقه خاص از آلگوريتمهاي تواني را براي شناسايي اعداد اول مشخص كنند، اين امكان پديد آمده كه به دنبال نمونه‌هاي بهتر اين روش بگردند. پومرانس و هندريك لنسترا از دانشگاه كاليفرنيا در بركلي با تلاش در همين زمينه توانسته‌اند زمان لازم براي محاسبات را از توان ‪ ۷.۵‬به توان ‪ ۶‬كاهش دهند.

اين دو از همان استراتژي كلي گروه هندي موسسه كانپور استفاده كردند اما تاكتيهاي ديگري را به كار گرفتند.

اگر فرضيه‌هاي ديگري كه درباره اعداد اول مطرح شده درست از كار درآيد آنگاه مي‌توان زمان محاسبه را از توان ‪ ۶‬به توان ‪ ۳‬تقليل داد كه در اين حد اين روش كارآيي عملي پيدا خواهد كرد.

در اين حالت يافتن اعداد اول با ‪ ۱۰۰۰‬رقم يا بيشتر به بازي كودكان بدل خواهد شد.

اما در نظر رياضي‌دانان مهمترين و جالبترين جنبه كار گروه سه نفره آ ك اس (كانپ.ر) روشي است كه آنان به كار گرفته‌اند.

اعداد اول براي رياضيات از اهميت بنيادين برخوردارند و هر نوع غفلت در فهم ويژگيهاي آنها باعث مي‌شود خللهاي بزرگ در بناي رياضيات پديدار شود.

روش اين سه رياضي دان هندي هرچند اين خللها و نقصها را پر نكرده حداقل به رياضي دانان گفته است كه در كجا به دنبال اين خللها بگردند.

آلگوريتم پيشنهادي اين سه محقق و همه انواع بديلي كه بر اساس آن ساخته شده متكي به وجود اعداد اولي با مشخصه هاي ويژه هستند. و در اغلب موارد استفاده از اين روش مستلزم آن است كه رياضي دانان اطلاعات دقيقي از نحوه توزيع اين قبيل اعداد اول خاص در ميان ديگر اعداد به دست آورند و به اين ترتيب جغرافياي مكاني اعداد اول را مشخص سازند.

روش پيشنهادي آ ك اس به رياضي دانان اين نكته را آموخته كه ويژگيهاي اين جغرافياي مكاني حائز اهميت است و نيز اين كه هنوز دانش كافي در اين زمينه به دست نيامده است.

در گذشته و در زماني كه نظريه اعداد تنها مورد توجه يك گروه كوچك از رياضي دانان بود ، اين مساله چندان اهميتي نداشت. اما در ‪ ۲۰‬سال گذشته اعداد اول موقعيتي استثنايي در عرصه رمز نگاري و دانش طراحي و شكستن رمزها كسب كرده اند.

رمزها صرفا از نظر نظامي و جاسوسي حائز اهميت نيستند بلكه از آنها در عرصه هاي تجاري و نيز فعالييتهاي اينترنتي در مقياس وسيع استفاده به عمل مي‌آيد. هيچ كس نمي‌خواهد كه راهزنان اينترنتي به اطلاعات شخصي مربوط به حسابهاي بانكي يا شماره كارتهاي اعتباري آنان دست يابد.

هم اكنون دزدي مشخصات شناسنامه اي افراد و جعل هويت آنان به صورت يكي از بزرگترين قلمروهاي فعالييتهاي تبهكارانه در سطح بين‌المللي در آمده است.

سازندگان كامپيوترها و ارائه‌دهندگان خدمات اينترنتي با توجه به آنكه در حال حاضر افراد بسياري از فعاليتهاي خود را از طريق اينترنت انجام مي دهند، نظير اينكه پول قبضهاي برق و آب و تلفن خود را مي‌پردازند يا در كلاسهاي مورد نظر ثبت نام مي‌كنند، يا بليت هواپيما و قطار رزرو مي‌كنند، در تلاشند تا از خطر دستيابي تبهكاران به اطلاعات شخصي افراد جلوگيري به عمل اورند.

يكي از مهمترين سيستمهايي كه در اين زمينه مورد استفاده صنايع است سيستم آر اس آ نام دارد كه متكي به اعداد اول است.

اعداد اول مورد استفاده در اين سيستم در حدود ‪ ۱۰۰‬رقمي هستند. سيستم آر اس آ در بسياري از سيستمهاي كامپيوتري مورد استفاده قرار دارد و در پروتكل اصلي براي ارتباطات امن اينرتنتي نيز گنجانده شده است و بسياري از دولتها، شركتهاي بزرگ و دانشگاهها از آن استفاده مي‌كنند. جواز استفاده از اين سيستم براي بيش از ‪ ۷۰۰‬شركت صادر شده و بيش از نيم ميليون كپي از آن در سطح جهاني مورد استفاده قرار دارد.

براي شكستن رمز آر اس آ بايد مضراب اعداد ‪ ۲۰۰‬رقمي يا بزرگتر را پيدا كنيد. هرچند فاكتور گيري يا عامل مشترك گيري از اعداد سخت تر از آزمودن اول بودن آنهاست اما اين دو مساله با يكديگر ارتباط دارند و رياضي دانان از يك ابزار براي حل هر دو مساله استفاده مي‌كنند.

همه اين جنبه‌ها بر اهميت كشف هر روشي براي محاسبه اعداد اول مي‌افزايد.

در سال ‪ ۱۹۹۵‬زماني كه پيتر شور از آزمايشگاههاي بل اثبات كرد كه مجموعه- اي از آلگوريتمهاي تواني براي فاكتور گيري وجود دارد، لرزه بر اندام بسياري افتاد.

اما خوشبختانه براي استفاده از اين آلگوريتم به كامپيوترهاي كوانتومي نياز است كه هنوز در مرحله تكميل تئوريك قرار دارند.

اكنون روش تازه آگراوال و دوستانش دوباره سيستم آر اس آ را در معرض خطر قرار داده است. آگراوال اكنون اين نكته را نشان داده كه مي‌توان با كامپيوتر هاي معمولي، اعداد را از حيث اول بودن مورد آزمايش قرار داد.

سوالي كه اينك مطرح شده آن است كه آيا الگوريتم مشابهي كه به صورت تواني كار كند براي فاكتورگيري اعداد غيراول نيز موجود است؟ پاسخ اغلب متخصصان به اين پرسش منفي است اما متاسفانه اين متخصصان همين حرف را در مورد آلگوريتم تواني مربوط به اعداد اول نيز مي‌زدند
در حال حاضر رياضي دانان واقعا مطمئن نيستند كه كه آيا چنين آلگوريتمي يافت مي‌شود يا نه.

اگر پاسخ مثبت باشد انگاه سيستم آر اس آ ديگر از امنيت برخوردار نيست.

يك عامل تخفيف‌دهنده نگرانيها آن است كه از سيستم آر اس آ براي انتقال همه محتواي پيامها استفاده نمي‌شود بلكه صرفا "كليد هاي رمز" را كه اندازه شان كوچك است با اين سيستم انتقال مي‌دهند.

براي انتقال بقيه پيام از روشهاي رمزنگاري متعارف بهره گرفته مي‌شود. به اين ترتيب جاسوسان در صدد برخواهند آمد كه به كليد رمزها دست يابند.

به اين ترتيب درسي كه از موفقيت گروه سه نفره هندي گرفته مي‌شود آن است كه بايد با احتياط در ارسال پيامها عمل كرد. اگر اكتشافات مشابه آنچه گروه كانپور بدست اورده تكرار شود، انگاه ديگر نمي‌توان به ايمن بودن ارتباطاتي كه روي اينترنت برقرار مي‌شود اطمينان داشت.

سلام  اين اعدادي كه ميبينيد ۵۰۰ تا عدد اول هستش. همينطور كه ميدونيد اعداد اول خيلي پيچيده هستند مثلا شكافهايي به اندازه دلخواه در آنها وجود دارد

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103,107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211,223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331,337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449,457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571,577,587,593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677,683,691, 701, 709,719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853,857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953,967, 971, 977, 983,991,997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097,1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217,1223,1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319,1321,1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451,1453,1459,1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571,1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693,1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811,1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949,1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017,2027, 2029, 2039, 2053, 2063,2069,2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137,2141, 2143, 2153, 2161, 2179,2203,2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269,2273,2281, 2287, 2293, 2297, 2309, 2311,2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377,2381,2383, 2389, 2393, 2399, 2411, 2417,2423,2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557,2579,2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689,2693,2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797,2801,2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917,2927,2939,2953, 2957, 2963, 2969, 2971, 2999, 3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079,3083, 3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187, 3191, 3203, 3209, 3217,3221,3229, 3251, 3253, 3257, 3259, 3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343,3347,3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433, 3449, 3457, 3461, 3463, 3467, 3469,3491,3499, 3511, 3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571.

در یک آزمایش جدید معلوم شد که ترس از ریاضیات می‌تواند شبکه‌های درد را در مغز فعال کند.

به گزارش ایسنا، متخصصان علوم پزشکی دانشگاه شیکاگو در این آزمایشات دریافته‌اند اضطراب ناشی از کلنجار رفتن با ریاضیات می‌تواند مناطقی را در مغز فعال کند که با تجربه به احساس دردهای جسمی و تشخیص تهدید غریزی، مرتبط هستند.

به گزارش سایت اینترنتی فیزورگ، این مطالعه به سرپرستی دکتر یان لیونز نشان داد در افرادی که هنگام مواجهه با مسائل ریاضی اضطراب شدیدی را تجربه می‌کنند، مناطقی از مغز که با احساس درد فیزیکی ارتباط دارند به فعالیت می‌افتند و هرچه این اضطراب و دلشوره بیشتر باشد این فعالیت عصبی نیز شدیدتر می‌شود و بنابراین احساس درد افزایش می‌یابد.

این متخصصان در بیانیه‌ای یادآور شدند: ما در این آزمایشات اولین مدرک عصبی را ارائه کرده‌ایم که نشان‌دهنده طبیعت تجربه فیزیکی مرتبط با ترس از ریاضیات است.

در مطالعات قبلی نیز نشان داده شده بود که سایر انواع استرس‌های روانی مانند انزوای اجتماعی و یا شکست عاطفی نیز می‌توانند احساس دردهای جسمی را در انسان بروز دهند اما در مطالعه جدید درواقع برای اولین بار واکنش درد مرتبط با حضور در یک موقعیت ایجاد اضطراب به جای خود حادثه استرس‌زا، آزمایش شده است.

در این آزمایش معلوم شد که حتی حضور در یک موقعیت ناخوشایند و نگران‌ کننده نیز پیش از اینکه حادثه‌ای رخ بدهد می‌تواند مناطق عصبی را با ایجاد درد جسمی ارتباط داده‌اند را فعال سازد و عملا احساس درد بدنی در انسان بوجود آورد.

این مطالعه در مجله پلوس وان منتشر شده است.

در سال ‪ ۱۹۸۳‬روشي كشف شد كه بسيار نزديك به روشهاي تواني بود. اين روش كه به وسيله سه رياضي دان به نامهاي لئونارد آدلمن از دانشگاه كاليفرنياي جنوبي، كارل پومرانس از آزمايشگاهاي بل در موري هيل نيو جرسي، و رابرت روملي از دانشگاه جورجيا كشف شد به نام خود آنان به روش آپي آر ‪ APR‬شهرت يافت.

در اين روش زمان محاسبه يك عدد داراي ‪ d‬رقم براي است با ‪.(d)ln ln d‬
در اين فرمول
(‪ (ln ln d‬به معناي لگارتيم لگاريتم ‪ d‬است. به لحاظ فني اين روش غير تواني است زيرا توان آن ثابت نيست و زياد مي‌شود. اما سرعت اين ازدياد بسيار بسيار كند است. يعني به ازاي ‪ d =10100‬ميزان ازدياد اين توان تنها ‪ ۵.۶‬مرتبه است. رياضي دانان به شوخي مي‌گويند كه ثابت شده اين توان به سمت بينهايت ميل مي‌كند اما چنين چيزي در عمل مشاهده نشده.

سوالي كه براي رياضي دانان مطرح است آن است كه آيا مي‌توان به روشي دست يافت كه به معناي دقيق و فني كلمه روشي تواني باشد. هيچ كس تصور نمي‌كرد كه احتمال چنين موفقيتي وجود داشته باشد تا اينكه گروه آگراوال بمب خود را منفجر كرد.

ايده انقلابي اين سه تن در سال ‪ ۲۰۰۲‬و زماني كه كايال و سكسنا هنوز دانشجوي دوره ليسانس بودند مطرح شد. در ابتداي سال جاري يك روايت بهبود يافته از روش پيشنهادي اين سه كه به آلگوريتم آ.ك.اس شهرت يافته در نشريه "آنالز او متمتيكس ‪ "Annals of Mathematics‬انتشار يافت.

اين آلگوريتم از نوع روشهاي تواني است و علاوه برآن بسيار ساده است (لااقل براي رياضي دانان چنين است). اين روش از اعقاب يك روش آزمون قديمي موسوم به قضيه كوچك پي‌ير فرما است.

اين قضيه را نبايد با قضيه اصلي فرما كه چند سال قبل پس از ‪ ۳۰۰‬سال اثبات شد اشتباه كرد. اين قضيه مبتني بر نوعي حساب متكي به قدر مطلق ‪modular‬موسوم به "حساب ساعت ‪ "clock arithmetic‬است علت آن تست كه در اين روش اعداد به شكل اعداد روي صفحه ساعت جمع مي‌شوند.

براي آشنايي با اين حساب خاص مورد زير را در نظر بگيريد. يك عدد دلخواه انتخاب كنيد و آن را قدر مطلق ‪ modulus‬بناميد. در مثال ساعت، اين عدد خاص كه قدر مطلق ناميده مي‌شود و مبناي محاسبه قرار مي‌گيرد، عدد ‪ ۱۲‬است.

حال در هر نوع محاسبه رياضي با اعداد صحيح براي تبديل آن سيستم عددي به سيستم عددي قدر مطلق ‪ ۱۲‬كافي است بجاي همه مضارب صحيح عدد ‪ ۱۲‬عدد صفر قرار داده شود. همه اعداد ديگر بر همين اساس تغيير مي‌كنند.

مثلا عدد ‪ ۲۵‬برابر است با ‪ . + ۲۴۱‬بنابراين عدد ‪ ۲۵‬در اين سيستم قدر مطلق برابر است با "‪ ۱‬به قدر مطلق ‪ ."۱۲‬سيستمهاي حساب متكي به قدر مطلق به تعريفي كه ذكر شد سيستمهاي زيبايي هستند زيرا در آنها همه قواعد حساب متعارف كار مي‌كند و درعين حال برخي از اعداد غيرصفر درآن ناپديد مي‌شوند.

قضيه كوچك فرما مي‌گويد اگر يك عدد اول را به عنوان قدر مطلق انتخاب كنيد ، داراي يك مشخصه ويژه خواهد بود. اين مشخصه عبارت از آن است كه يك فرمول خاص يعني ‪ (a)p-1‬در اين سيستم همواره برابر يك خواهد بود.

در اين فرمول ‪ p‬عبارت است از عدد اولي كه به عنوان قدر مطلق انتخاب شده و ‪a‬هر عدد ديگر است كه ضريب ‪ p‬محسوب نمي‌شود.

اگر مقدار فرمول بالا برابر يك نباشد آنگاه عددي كه به عنوان عدد اول تصور كرده بوديد يعني ‪ p‬عدد اول نيست.

به اين ترتيب مي‌توان از اين قضيه كوچك فرما به عنوان مبنايي براي تدوين آزموني جهت تعيين اعداد اول استفاده كرد. اين آزمون كاملا بي‌نقص نيست زيرا شماري از اعداد غير اول نيز از غربال آن رد مي‌شوند.

اما مي‌توان روايت هاي پيچيده تر و دقيق تري از اين آزمون را توليد كرد كه بسادگي به اعداد غير اول اجازه ورود ندهند. يك نمونه پيشرفته از اين آزمونها همان روش "آ.پي.آر" است كه در بالا اشاره شد.

گروه آگراوال از همين قضيه كوچك فرما استفاده كرد اما آن را به نحو ديگري بسط داد. اين گروه به عوض آنكه با اعداد كار كنند از چند جمله‌اي‌ها استفاده كردند.

چند جمله‌اي‌ها عباراتي جبري هستند نظير (‪ .a + b(2‬ايده استفاده از اين روش محصول كوشش آگراوال در دوراني بود كه بر روي رساله دكتري خود كار مي‌كرد و به اتفاق استاد راهنماي خويش "سومنات بيسواس" در سال ‪ ۱۹۹۹‬مقاله- اي را به چاپ رساند كه در آن يك روش آزمون اعداد اول پيشنهاد شده بود كه از همين چند جمله‌اي‌ها استفاده مي‌كرد و به شيوه احتمالاتي محاسبات را انجام مي داد.

آگراوال بر اين باور بود كه مي‌تواند اين روش پيشنهادي را دقيق‌تر و عنصر احتمالاتي آن را حذف كرد.

در سال ‪ ۲۰۰۱‬دو تن از دانشجويان او يعني كايال و سكسنا به يك نكته بسيار حساس و فني توجه كردند. ابتدا اين مساله سبب شد تا گروه سه نفره در آبهاي عميق نظريه اعداد غوطه ور شوند، اما اندك اندك برايشان روشن شد كه تنها يك مانع در راه تكميل روشي جهت آزمودن دقيق و سريع اعداد اول وجود دارد.

مانع از اين قرار بود كه روش آنان تنها در صورتي كار مي‌كرد كه عدد اول مورد نظر كه با ‪ p‬نمايش داده مي‌شود همواره در محدوده خاصي جاي داشته باشد كه با اعدادي كه در آزمون شركت داده مي‌شوند مرتبط باشد.

مشخصه ويژه اين مانع آن است كه عدد " ‪ "p-1‬بايد يك مقسوم عليه يا بخشياب بسيار بزرگ باشد.

ادامه دارد...

http://www.irna.ir/fa/news/view/menu-279/8405190499170629.htm